מערכת השמש שלנו, כמו מערכות רבות אחרות, מורכבת מגופים שמקיפים גופים כבדים מהם. כוכבי הלכת מקיפים את השמש, הירחים מקיפים את כוכבי הלכת, ובמקרה של כדור הארץ מקיפים אותו גם לוויינים מלאכותיים ותחנת חלל.
הכוח שמניע את התנועה הזאת הוא כוח הכבידה. אנו נוהגים לחשוב על התנועה הזו בצורה פשוטה מאוד. נוח לנו לדמיין את כדור הארץ נע במסלול מעגלי מסביב לשמש כאשר השמש אינה זזה ממקומה כלל, אך בפועל התמונה מורכבת יותר. המסלולים אינם מעגלים מושלמים, וגם הגופים הכבדים יותר (השמש לעומת כדור הארץ, כדור הארץ לעומת הירח וכו') נעים מעט בהשפעת הגופים הקטנים מהם.
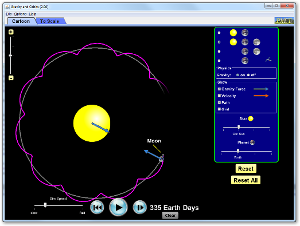
התנועה הזאת נשלטת בידי כוח הכבידה בין הגופים. היישומון שלפנינו יאפשר לנו לחקור מעט את התנועה הזאת, לקבל תחושה על המסלולים האפשריים ולגלות איך תנאי ההתחלה של התנועה משנים אותם. להפעלת היישומון לחצו על התמונה.
היישומון הופק במסגרת פרויקט PhET של אוניברסיטת קולורדו
להורדת היישומון ולהרצתו על המחשב לחצו כאן
אם אינכם מצליחים להעלות את היישומון, התקינו את תוכנת Javaweb. לחצו כאן והתקינו לפי ההוראות.
היישומון פשוט יחסית להפעלה. בסרגל שמימין תוכלו לבחור באחת מהמערכות השונות שעליה תסתכלו. ההבדל בין המערכות הוא בסדרי הגודל של המרחקים והמסות של הגופים. המערכת היחידה השונה במקצת מהאחרות היא זו שמורכבת משלושה גופים – השמש, כדור הארץ והירח. אני ממליץ לכם להתחיל במערכת פשוטה של שני גופים (לדוגמה כדור הארץ והירח) ולהמשיך הלאה רק אחרי שתרגישו שהבנתם אותה.
בשלב הראשון הסתכלו על המערכת בקנה מידה אמיתי כדי לקבל תחושה של הגדלים והמסות האמיתיים. ולאחר מכן עברו לקנה מידה "אילוסטרציה", שמאפשר הפעלה פשוטה יותר של היישומון.
התחילו את היישומון כך שתראו בו רואים את וקטורי המהירות וכוח הכבידה. תוכלו לראות מיד את התופעה שציינו למעלה. במבט ראשון נראה שהירח מסתובב סביב כדור הארץ, אולם בפועל גם כדור הארץ עצמו מסתובב ושני הגופים נעים בתנועה מחזורית סביב מרכז המסה שלהם. מאחר שמסת כדור הארץ גדולה ממסת הירח בערך פי אלף, הנקודה הזו קרובה מאוד למרכז כדור הארץ.
אם תעברו למערכת של כדור הארץ ותחנת החלל, מסת כדור הארץ כבר תהיה גדולה פי 16 מיליארד מזו של תחנת החלל, ולכן נקודת מרכז המסה תהיה קרובה למרכז כדור הארץ עד כדי כך שלא תוכלו לזהות עוד שכדור הארץ נע. תוכלו לחזור על הניסוי במערכות שונות עם מסות שונות ולראות איך היחס בין המסות משפיע על מקומה של נקודת מרכז המסה וכתוצאה מכך על התנועה של שני הגופים. נסו לדמיין מה היה קורה אילו לשני הגופים היתה מסה זהה.
כעת הגיע הזמן לבדוק את צורת המסלול. לשם הנוחות בחרו במערכת עם מרחקים גדולים והבדל מסות גדולה – לדוגמה השמש וכדור הארץ. התחילו את התנועה ועיקבו אחר המסלול. תוכלו לראות שהמסלול כמעט מעגלי, עם סטיות קלות מהמסלול המעגלי.
כעת נסו לשנות מעט את המערכת. תוכלו לגרור את כדור הארץ למרחק שונה מהשמש או לשנות את המהירות ההתחלתית של כדור הארץ. בחנו איך הדבר משפיע על התנועה. אם הצלחתם ליצור תנועה מחזורית, כלומר הקפה של כדור הארץ סביב השמש אך במסלול שונה ממעגל, נסו לחשוב מהי הצורה שנוצרה והעלו את זה לדיון בפורום.
שימו לב שתנועה מעגלית מושלמת דורשת תנאי התחלה מאוד נוקשים. המהירות חייבת להיות מאונכת לכוח הכבידה, אך גם נדרש שגודל המהירות יהיה גודל מסוים שתלוי במרחק של כדור הארץ מהשמש. לכן כל שינוי קל בתנאי ההתחלה יגרום לסטייה מהתנועה המעגלית. אם מערכת השמש נוצרה באופן מקרי וספונטני, קשה מאוד לדמיין מצב שבו תנאי ההתחלה היו כל כך מדויקים, ולכן תנועת הגופים אינה מעגל מושלם.
נסו להפעיל את היישומון בתנאים שונים. אם אתם מוצאים תנאים מעניינים במיוחד, ספרו לנו עליהם בפורום.
ירון גרוס
המחלקה לפיסיקה של חומר מעובה
מכון ויצמן למדע
הערה לגולשים
אם אתם חושבים שההסברים אינם ברורים מספיק או אם יש לכם שאלות הקשורות לנושא, אתם מוזמנים לכתוב על כך בפורום ואנו נתייחס להערותיכם. הצעות לשיפור וביקורת בונה יתקבלו תמיד בברכה.